From:堀口寿人
英語には、こんな言葉がある。
「自分が考えていること=自分という存在である」という意味だ。つまり、あなたという存在は思考が反映されたものだという意味。
それくらい、思考は僕たちにとって、あまりに重要だ。
でも・・・
思考は、あまりに僕たちにとって馴染み過ぎていて、「思考とは何?」と聞かれてもはっきり答えられない。目にも見えないし。
そこで、この記事では、まず「思考とは何か?」を明らかにする。さらに・・僕たちは、日ごろどんな思考を使っているのかを見ていこう。
この記事で、思考の意味や思考力、論理的思考といった言葉の意味がよく理解できるはずだ。
思考とは何か?
思考の意味-辞典より
アメリカ心理学会が発行するAPA心理学大辞典によると、思考の意味は次のように解説されている。
発想やイメージ、心的表象、あるいは他の仮説的な思考の要素が経験・操作される認知的活動。
思考は次の2つの特徴を持つ
隠されたもの、すなわち直接的には観察できないが、行動や自己報告から推測されうること
象徴的なもの、すなわちその本質については、未だあいまいで議論を呼ぶような、心的な象徴や表象の操作を伴うものであるということ
つまり、アメリカ心理学会ですら、「思考はあいまいだ」と言っているわけだ。
もう一つ。別の視点から思考を説明したものがある。認知心理学(ミネルヴァ書房)という本だ。その本の言葉を借りると、思考は次のような意味になる。
思考の本質は推論。推論とは、ある前提から結論を導く精神活動。
さっきよりも、スッキリ分かりやすくなった。要するに、思考とは「すでにある情報から新しい情報を導き出す心の活動」という意味だと思えば大丈夫だろう。
論理的思考とは
「論理的」という言葉は、思考とよくセットで使われる。せっかくなので、論理的というのもどういう意味か調べてみた。次はAPA心理学大辞典から抜粋したものだ。
妥当な結論が一般に認められた前提から導き出されるという論証の形式に関わる認識論の下位領域
このままだと何かよく分からない・・・。ま、要するに、「どうやってすでにある情報から新しい情報を導き出すか?」という、導き出し方の形式と思ってもらえれば十分だろう。
イメージ的に言うと、「こうだからこう、こうだからこう、だから結果的にこうなりますよ」といった考え方の形式のことだと思えばいいだろう。
これに関しては、後で4つの形式を順番に見ていくので、お楽しみに。
思考力とは
それと思考力という言葉もよく使われる。ただ、思考力という言葉は専門的な言葉じゃない。思考力とは、僕たちが普通に使う俗語だ。
だから、辞典には思考力の意味は載っていない。だけど、ここまで見てきたあなたなら、こう意味づけするだろう。
思考力とは、「すでにある情報から新しい情報を導き出す力」と。ま、その程度の意味で十分だろう。
つまり思考の意味は?
思考とは、「すでにある情報から新しい情報を導き出す心の活動」だ。じゃあなぜ僕たちは、すでにある情報から新しい情報を導き出そうとするのか?
それは、問題解決のためだ。
僕たちは、いつだって、よりよくなりたいと考えている。だから思考するわけだ。というわけで次に4つの論理的思考を見ていこう。僕たちは、いつもこのどれかの形式で試行している。
思考1:演繹的思考

これは、演繹的(えんえきてき)思考と読む。言葉は難しいが、意味は簡単だ。
演繹的思考は、自明の真実からスタートして、結論を導き出す論理だ。
例えば、こういう例はどうだろう。
- 昆虫は6本足(前提1)
- クモは8本足(前提2)
「昆虫は6本足」というのは自明の真実だ。このことに関しては、あなたも僕も反論しようがないだろう。「クモが8本足」というのも同じだ。自明の真実になる。
この2つの前提から導き出せる結論はこれだ。
- だから、クモは昆虫でない(結論)
前提2つが自明の真実だから、結論にも説得力がある。これが俗にいう三段論法だ。演繹的思考には、定言的思考と条件的思考の2種類がある。
定言的思考
定言的思考というのは、前提に「全ての」とか「ある」といった量を表す表現が含まれているパターンの思考だ。
定言的思考は、さらに単純なものと複雑なものがある。
単純な定言的思考
- 全てのAはB(前提1)
- 全てのBはC(前提2)
というようなパターンだ。前提1と前提2からどんな結論が導き出せるだろう?
簡単に考えて欲しい。答えはこれだ。
- よって全てのAはC(結論)
図で表すとこんな感じだ。
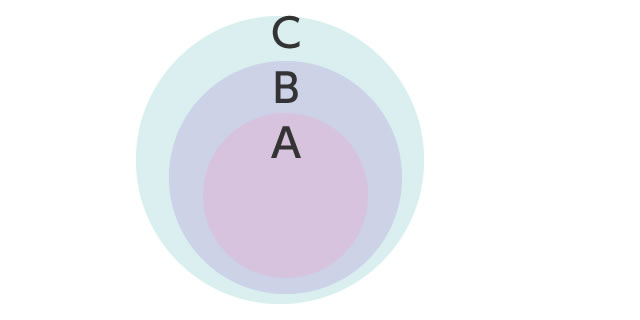
勘のいいあなたはすぐに分かったかもしれない。ただ、次のはもう少し難しい。
複雑な定言的思考
- どのAもBでない(前提1)
- 全てのBはC(前提2)
さて、この2つの前提から、何が言えるだろう?
答えはこれだ。
- あるCはAでない
「なんじゃそりゃ?」と思ったかもしれない。これが、なぜさっきのより複雑なのか?図で見てみるとそれがよく分かる。
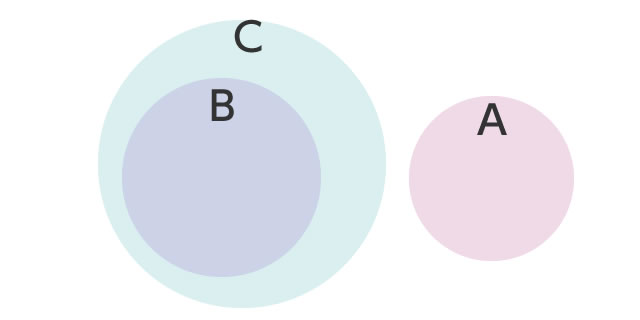
というパターンも考えられるし・・・
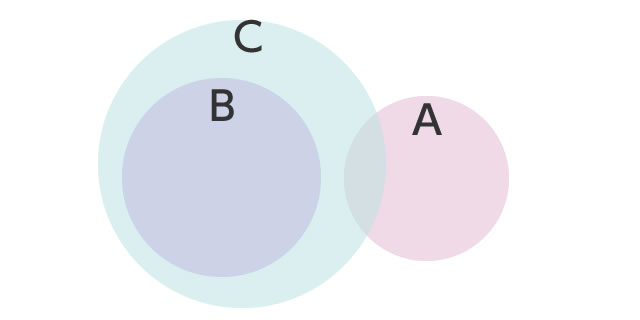
というように、AとCが重なっているパターンも考えられる。要は、単純なケースよりあいまいになっているわけだ。だからその分難しい。
条件的思考
演繹的思考の2つ目は条件的思考だ。条件的思考は前提に「もし~ならば」という条件分が含まれる。
条件的思考も、さらに肯定式と否定式の2種類に分けられる。否定式の方が難しい。まずは簡単な肯定式からだ。
肯定式
- もしpならばq(前提1)
- pである(前提2)
- よってqである(結論)
これだけだと、「はあ?何のこと?」という感じもあるだろう。だから具体例で考えてみよう。こんな例はどうだろうか?

- もし20歳なら飲酒できる(前提1)
- 20歳である(前提2)
- よって飲酒できる(結論)
こうやって考えれば、そんなに難しいと感じないだろう。じゃあ、次に否定式を見てみよう。
否定式
- もしpならばq(前提1)
- qではない(前提2)
この2つの前提から導き出せる答えはこうだ。
- よってpでない(結論)
また、飲酒の例で考えてみよう。
- もし20歳なら飲酒できる(前提1)
- 飲酒できない(前提2)
- よって20歳ではない(結論)
他の組み合わせ
ちなみに、今説明した肯定式と否定式以外にも、次のような2つの組み合わせが考えられる。
<3番目の例>
- もし20歳なら飲酒できる(前提1)
- 飲酒できる(前提2)
- よって20歳である(結論)
この論理はよく考えてみると、間違いだと分かる。飲酒できる年齢は20歳だけじゃない。32歳かもしれないし、48歳かもしれないし、75歳かもしれない。
<4番目の例>
- もし20歳なら飲酒できる(前提1)
- 20歳でない(前提2)
- よって飲酒できない(結論)
この論理もよく考えると間違いだと分かる。20歳でないとしても、20歳未満とは限らない。32歳かもしれないし、48歳かもしれないし、75歳かもしれない。
演繹的思考に挑戦
じゃあ、実際に演繹的思考に挑戦してみよう。まず、次の4枚のカードを見て欲しい。

これらは、表にアルファベット、裏に数字が印刷されているカードだ。
これらのカードについて「もし表がBなら、裏は2」というルールが正しいかどうかを調べたい。そのためには、どのカードをめくって反対側を調べればいいか?
ちょっと難しいので、もし時間があれば、この状態で下にスクロールせずに考えてみて欲しい。
・・・
ヒントは、「ルールが間違っていると証明するにはどうしたらいいか?」と考えればいい。
・・・
どうだろう?何となく答えは出ただろうか?それでは、答え合わせだ。
答えは、
Bと5。
まずBである理由から。もしBの裏が2以外なら、ルールの間違いを証明できる。次に5である理由。もし5の裏がBなら、ルールの間違いを証明できる。
じゃあ、なぜ“2”じゃダメなのか?
その理由は、もし2の裏がBだったとしても、ルールが正しいことを証明できるだけだ。もしかして他のカードではルールが成立していないかもしれない。その可能性を残してしまう。
もし2の裏がCとかDとかだったとしても、ルールの間違いを証明できない。というのも、ルールは「もし表がBなら、裏は2」としか言っていないからだ。「裏が2なら、表がB」とは言っていない。だから、表は何だったとしても、ルールの間違いを証明できないわけだ。
思考2:帰納的思考
帰納的思考というのは、いくつかの事例から一つの結論を導く思考論理だ。

例えば、
- カラスAは黒い(事例1)
- カラスBは黒い(事例2)
- カラスCは黒い(事例3)
- よってカラスは黒い
というように。僕たちが他人を判断するときも、帰納的思考の論理を使っている。
例えば、
- Aさんは、よく愚痴を言う(事例1)
- Aさんは、ほとんど笑わない(事例2)
- Aさんは、友達が少ない(事例3)
- よってAさんは人間的に欠陥がある(結論)
という感じだ。だいたい想像できると思うが、帰納的思考で出した結論は「絶対正しい」と言い切れるものじゃない。
まあ、「おそらくそういう傾向があるでしょう」という程度のものだ。そういう意味では演繹的思考の結論とは違う。帰納的思考にも次の2種類がある。
不完全帰納
不完全帰納とは、一般的な帰納的思考のことだ。つまり、さっきのカラスの例とか、他人判断の例とかがそうだ。
僕たちが生きている世の中では、あるテーマに関する事例を全部集めることはたいてい不可能だ。だから、一部の事例を集めて、そこから全体を推測するという方法を取る。
それが、不完全帰納の考え方だ。これとは逆なのが完全帰納だ。
完全帰納
完全帰納では、あるテーマに関する事例を完全に集めつくして、結論を出す。だから、完全帰納で出した結論は絶対的に正しい。
ただ、さっきも言ったように、僕らの社会では、あるテーマについての事例を全部集めつくすのは、普通ムリだ。
例えば、さっきの他人を判断する場合も、完全帰納をしようと思えば、その人に関する情報を全部集めつくさないと行けない。いかに無謀か分かるだろう。
だから、たいてい帰納的思考と言えば、不完全帰納を意味する。
帰納的思考に挑戦
今から僕が「あるルール」にそって、3つの数字のセットを順番に挙げていく。あなたにやってもらうことは、「どんなルールが背景にあるか」を当ててもらうことだ。
まずは・・・
2 4 6
だ。この3つの数字は、僕が決めた「あるルール」に従って、並んでいる。こんな感じで、3つの数字のセットを次々お見せしていく。
次は・・・
4 6 8
だ。どうだろう?これもさっきのセットと同じルールに従って並べてある。こんな感じで次々行こう。
10 12 14
どうだろう?何となくルールを思いつてきたかな?
1 3 5
あれ?と思わなかっただろうか?でも、僕は「そのルール」を変えていない。最初と同じルールに従っている。あと2回ぐらい行こうか。
8 9 10
さて、どうだろう?ちょっと混乱してきたかもしれないね。でも、くどいようだが、僕はルールを変えていない。では、もう一つ。
11 15 16
さて、どうだろう?ルールは見えただろうか?
じゃあ、正解の発表だ。僕が持っていた「あるルール」とは・・・
「右に行くほど数字が増える3つの数字」だ。ただ、それだけ。ちょっとガッカリしたかもしれないけど、まあこれはゲームなんで。
ちなみに、このゲームに正解するかどうかはあんまり大事じゃない。大事なのは、「今あなたが帰納的思考を体験的に理解した」ということだ。そのことに価値がある。
思考3:類推
次は類推(るいすい)だ。類推とは、ある知っているものから、知らないものを推測するという思考論理だ。
このとき、すでに知っている情報をベース、新しく知ろうとする情報をターゲットという。
例えば、僕は前に、心の流れを説明するのにライン作業の例えを使った。
ライン作業というのは目に見えるものだし、あなたもイメージができるだろう。ただ、心の流れは目に見えないもので、僕たちにはよく理解しにくいものだ。だから、ライン作業によって心を類推したわけだ。

このとき、ベースが「ライン作業」、ターゲットが「心」ということになる。詳しくは、「集中力とは?集中力の意味を例え話で解説」の記事を参考にして欲しい。
思考4:確率的思考
最後の思考論理が確率的思考だ。これは、出来事が起きる確率を推測するときの思考論理だ。
女性の例え

あるところに、リンダという女性がいた。彼女は大学時代、福祉施設でボランティアをしていた。
そんな彼女も、大学を卒業して10年になる。さて、彼女は今どうしているだろう?次の2つから確率が高いと思う方を選んでほしい。
- 結婚して主婦をしている
- 結婚して主婦をしていてボランティアも続けている
どっちか選べただろうか?
では、答え。
答えは・・・
1番だ。
2番の方が確からしく思える。でも、1番は2番の内容も包括しているわけで、1番の方が可能性が高くなる。
つい、僕たちは確からしい方を選んでしまうという例だ。じゃあ、同じ系統でもう一つの例。
コインの例え

コインを4回投げて、表が出るか、裏が出るかを調べる。このとき、次のどっちの可能性が高いだろう?
- 表表表表
- 裏裏表裏
どっちか選んだだろうか?
それでは、答え合わせ。
答えは・・・
「どっちも同じ確率」でした。正解したかな?
結局、1回あたり裏が出る確率と表が出る確率は一緒だ。ということは、それを4回繰り返しても同じというわけだ。
パッと見、2番の方が確からしい。でも、確率は同じというわけ。じゃあ、最後にちょっと難しい問題。
感染病の例え
まず、次の内容をよく読んでほしい。
内容を理解できただろうか?
では、スクロールする前に、確立を考えてみて欲しい。
・・・
OK?では、確率の正解を順を追って見てみよう。
まず、1000人の人がいたとして、
- 実際に感染している人は1人
- 感染していない人は999人
となる。次に、「感染していないのに陽性となる確率が5%」ということなので、感染していない999人を考える。このとき・・・
- 陽性反応が出るのは約50人(間違いの陽性)
- 陰性反応が出るのは約950人
となる。ちなみに感染している人は当然陽性と出るはずだ。
ということは、陽性と出るのは1000人中・・・
- 実際に感染している1人
- 感染していない約50人(間違いの陽性)
というわけだ。つまり、陽性と診断された人の中で、実際に陽性の人の確率は、1/50=2%ということになる。
この例えが難しいところは、1/1000と5%という形で確率が2重に絡んでくるところだ。面白い事に僕たちは、1/1000という数字を無視して考えがちだ。
まとめ
思考とは、「すでにある情報から新しい情報を導き出す心の活動」だ。そして、論理とは、思考するときの形式のことだった。